The Mean Value Theorem

Engineering Context:

MAE/ECE: Police officer’s radar guns use principles like the Mean Value Theorem to determine if people are speeding over a given distance. For example, say a car is traveling on a road with a speed limit of 60mph. It passes a radar gun at 1:00 pm and is going 55 mph. 30 minutes later, it passes a second radar gun 35 miles down the road and is going 57 mph. According to the two separate readings, the car is not speeding. However, if you calculate the average speed the car must have traveled at between the first radar gun and the second by dividing 35 miles by .5 hours, you find an average speed of 70mph. The Mean Value Theorem states that, since the average between the two points is 70mph, the car must have been traveling exactly 70mph at some point between the radar guns. Thus, the car could get ticketed for speeding even though a speed over 60mph was never directly measured. Mechanical and electrical engineers could work together to design a radar gun that could measure someone’s speed and provide that information back to the police officer.

BENG: When a biological engineer is looking at a graph of bacteria growth, it might be convenient to know the mean value theorem. This could help them find times where the rates of growth differs from the average rate of growth and make necessary adjustments to bacteria conditions.

CEE: Civil and environmental engineers care about the mean value theorem and its applications to air pollution. A car’s gas mileage is based on the mean value theorem. Your car tells you an average gas mileage over a period of time. At some points the car will get fewer miles per gallon, and at some points it will get more miles per gallon. Environmental engineers could use the average gas mileage information to predict and counteract the pollution caused by the car.

The Essentials

The Mean Value Theorem states that if a function f is continuous over [a,b] and differentiable over (a,b), then at some point, c, along the function, the average slope of f over [a,b] is equal to the instantaneous slope at f(c).

f ′ c = f b - f a b - a
the mean value theorem

Figure 1: y = x − 3 3 + 2 x − 3 2 + 1

In Figure 1 the blue line represents the average velocity over the interval 1 4 . The dotted green lines show the points on the graph whose tangent lines have the same slope at the average velocity line.

There is also a Mean Value Theorem for Integrals. This theorem guarantees that if f(x) is continuous, then there exists a point c whose value is equal to the average value of the function f(x) over a b .

∫ a b f x d x = f c b − a
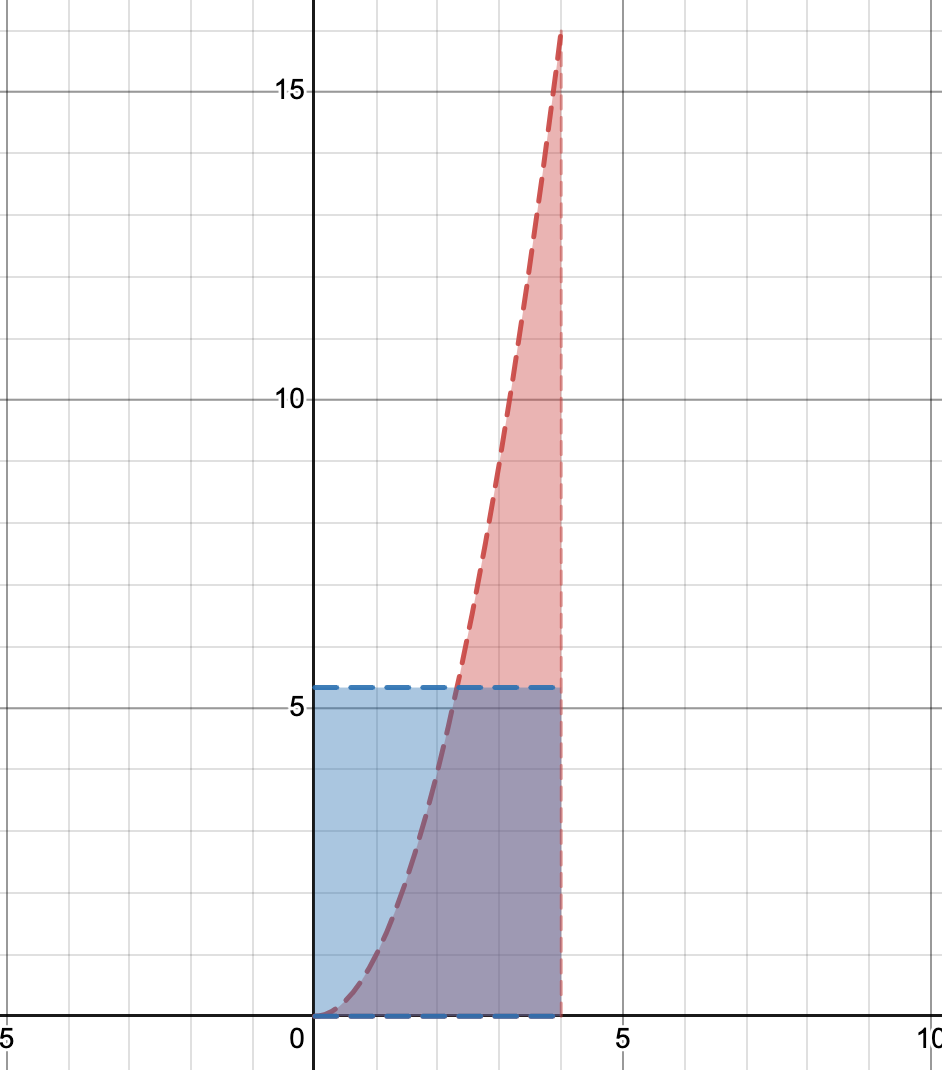
the mean value theorem for integrals

Figure 2: y = x 2 0 4

In Figure 2 the area under the curve y = x 2 (shaded in red) is the same as the area of the rectangle shaded in blue. The point where these two lines intersect is the point (c, f(c)). This point was found using the Mean Value Theorem for Integrals.

A Deeper Dive

The Mean Value Theorem originated in the late 1600’s when Michel Rolle developed an early version of it. The Mean Value Theorem for integrals informs the derivation of many other theorems in introductory calculus, such as the Fundamental Theorem of Calculus. It also serves as the basis of many of the concepts in more advanced math and engineering classes. While it may seem obsolete in practice today, the Mean Value Theorem was incredibly crucial to the development of calculus.

This is just one example of the use of the Mean Value Theorem in the proof of the Fundamental Theorem of Calculus.

F ′ x = lim h → 0 f x + h − f x h
F ′ x = lim h → 0 1 h ∫ a x + h f t d t − ∫ a x f t d t
F ′ x = lim h → 0 1 h ∫ a x + h f t d t − ∫ x a f t d t
F ′ x = lim h → 0 1 h ∫ x x + h f t d t

Since we are working over the interval [x,x+h], The Mean Value Theorem states:

1 h ∫ x x + h f x d x = f c
F ′ x = lim h → 0 1 h ∫ x x + h f x d x

Since c approaches x as h approaches 0, we have:

F ′ x = lim h → 0 f c
F ′ x = f x

The Fundamental Theorem of Calculus is central to all of calculus because it helps us to connect differentiation and integration. Since the Mean Value Theorem is one of the building blocks of the Fundamental Theorem of Calculus, it too is essential to the foundation of calculus.

Practice

Exercise 1. Using the Mean Value Theorem, find a point c whose instantaneous velocity is equal to the average velocity over the interval [-1,2].

f x = x 2

Exercise 2. Use the Mean Value Theorem for Integrals to identify a point c whose value is equal to the value of y = 3 x 2 over 0 3

Solutions:

Exercise 1.

First find the average velocity over the interval.

4 − 1 2 − −1 = 3 3 = 1

Then find a point c whose slope is equal to 1 by taking the derivative of f(x).

1 = 2 x

At x = 1 2 the slope is equal to the average slope over -1 2

Exercise 2.

Plug it into the formula above and solve for c

∫ 0 3 3 x 2 d x = 3 c 2 · 3 - 0
27 = 9 c 2
c = √ 3

More Resources