Contact Info

Location Engineering Building | room 332
Phone 435-797-1494
Contact Christian Bolander
Email christian.bolander@usu.edu

Hours

Mon–Thu	10am – 5pm
Fri	10am – 4pm

Drop-Ins Welcome!

Closed weekends and university holidays.

Limits

A value is said to be a limit of another value if the latter can approximate the former nearer than any given value, no matter how small it may be supposed, however, without the approximating value being able to exceed the value it approximates.

(Jean le Rond D’Alembert, Encyclopédie méthodique ou par ordre de matières, 1765)

When the successive values attributed to a variable approach a fixed value indefinitely, so as to end by differing from it as little as wished, this fixed value is called the limit of all others.

(Augustin-Louis Cauchy, Cours d’Analyse, 1821)

Engineering Context

Limits provide the basis of our understanding of how systems change over time, and are formally used when taking derivatives. Additionally, numerical simulations often require applications of limits. Most numerical simulations seek to approximate a physical medium using discrete chunks, such as cubes or polyhedrons. Put simply, the numerical solution is considered to be an appropriate (in terms of the physics used) approximation of the true answer in the limit as those chunks become infinitely small. In this way, limits can be used less-formally to look at trends in data and determine an ideal amount of subdivisions to be used to solve the problem.

MAE:

(1) Estimation of the velocity v based on position y with respect to time t

v (t) = lim_{∆t \to 0} \frac{y (t + ∆t) - y (t)}{∆t}

(2) Determining the number of grid points to use in the simulation of a wing to give an accurate representation of lift

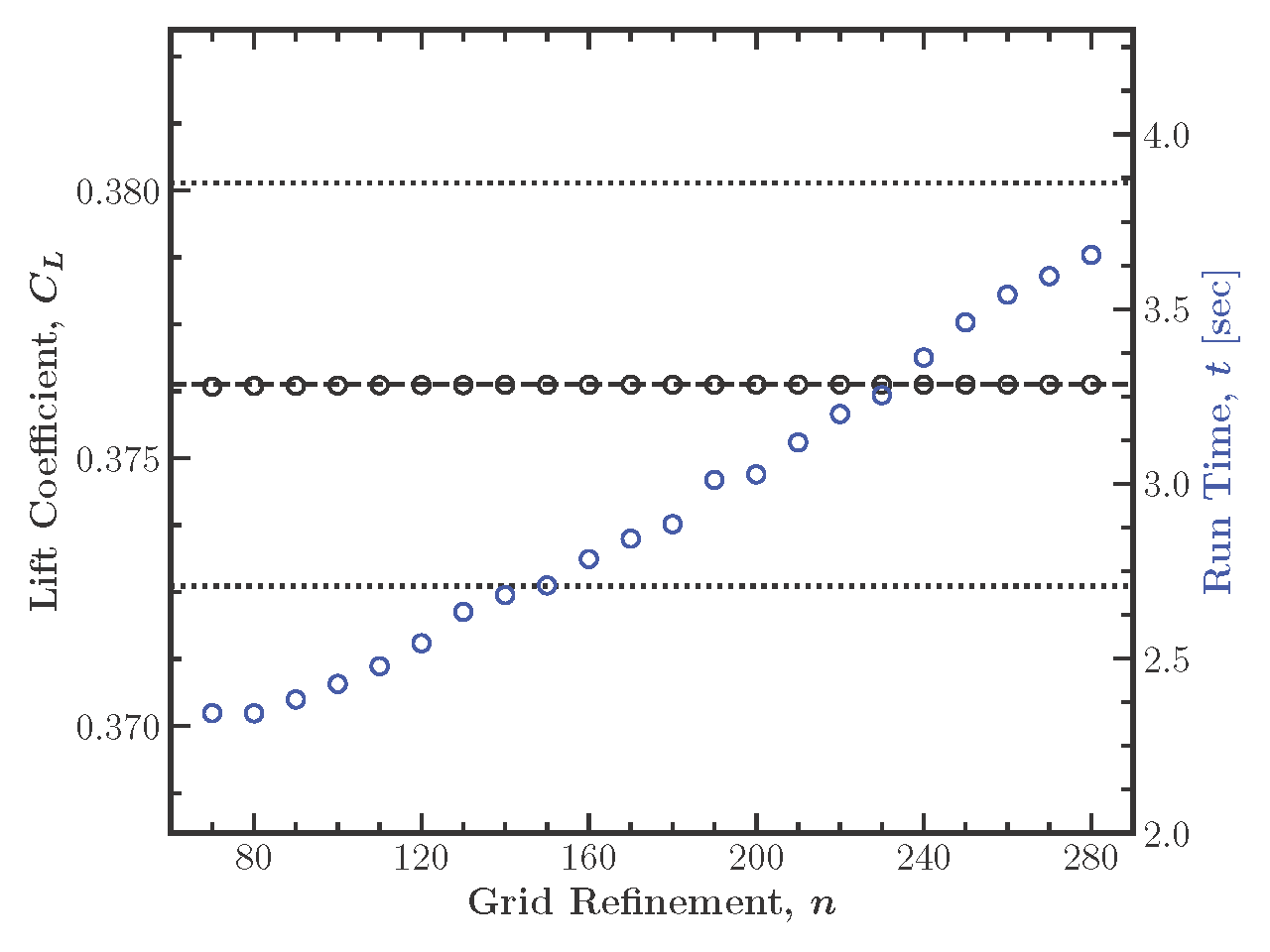
$Figure 1$

Figure 1: Recognizing that the number of grid points doesn’t affect the lift coefficient allows an engineer to choose a simulation with a shorter run time.

ECE:

(1) Estimation of the voltage v based on electrical potential energy w with respect to charge q

v (t) = lim_{∆q \to 0} \frac{w (q + ∆q) - w (q)}{∆q}

BE:

(1) Rate of change of energy at an instant in time

\frac{dE}{dt} = lim_{∆t \to 0} \frac{∆E}{∆t} = \hat{M_{i}} h_{i} + \hat{M_{o}} h_{o} - \hat{Q} + \hat{W_{s}}

CEE:

(1) Finding the shear force V based on a bending moment M with respect to distance along a beam x

V (x) = lim_{∆x \to 0} \frac{M (x + ∆x) - M (x)}{∆x}

The Essentials

A limit is the output that a function (or sequence) approaches as the input (or index) approaches a given value.

General Form:

lim_{x \to a} f (x) = L

Two Fundamental Limits:

lim_{x \to a} x = a

lim_{x \to a} c = c

where a is a real number and c is a constant.

One-Sided Limits:

lim_{x \to a^{-}} f (x) = L

lim_{x \to a^{+}} f (x) = L

Relating Two-Sided and One-Sided Limits:

Theorem. Let f(x) be a function defined at all values in an open interval containing a, with the possible exception of a itself, and let L be a real number. Then,

lim_{x \to a} f (x) = L iff lim_{x \to a^{-}} f (x) = L and lim_{x \to a^{+}} f (x) = L

Infinite Limits From the Left:

If f(x) increases without bound as x approaches a from the left

lim_{x \to a^{-}} f (x) = + \infty

If f(x) decreases without bound as x approaches a from the left

lim_{x \to a^{-}} f (x) = - \infty

Infinite Limits From the Right:

If f(x) increases without bound as x approaches a from the right

lim_{x \to a^{+}} f (x) = + \infty

If f(x) decreases without bound as x approaches a from the right

lim_{x \to a^{+}} f (x) = - \infty

Two-Sided Infinite Limits:

If f(x) increases without bound as x approaches a

lim_{x \to a} f (x) = + \infty

If f(x) decreases without bound as x approaches a

lim_{x \to a} f (x) = - \infty

A Deeper Dive

When dealing with limits, engineers are hoping to understand how a function behaves around specific points. When looking at the symbolic description of the limit of a function, given as

lim_{x \to a} f (x) = L

we can first direct our attention to the subscript under the lim operator. In words, this is read as “the limit as x approaches a”, which indicates that the variable x is approaching some number a. As that happens, the value of the function at x, f(x) will eventually get to L when x = a.

Consider the plots in Figure 2. Each of the functions plotted have a discontinuity at x = 1 and are undefined at that location. In these cases, we need as much information as we can about the function to make informed decisions about its behavior. However, we can see that these functions have well-defined behavior as they get nearer to x = 1 and can present that information using the following concepts.

One-Sided Limits: We can look at the limit as we move to x = 1 from the left- or right-hand sides of the plot. These are called one-sided limits and are written as

lim_{x \to a^{-}} f (x) = L

(Limit from the left)

and

lim_{x \to a^{+}} f (x) = L

(Limit from the right)

One-sided limits can also be used to prove that the limit exists at a given point using the following Theorem.

Theorem. Let f(x) be a function defined at all values in an open interval containing a, with the possible exception of a itself, and let L be a real number. Then,

lim_{x \to a} f (x) = L iff lim_{x \to a^{-}} f (x) = L and lim_{x \to a^{+}} f (x) = L

In other words, if the limit from the left and the limit from the right are the same, that is the limit of the function at that point! Figure 2b is a great example of an application of this theorem.

Infinite Limits: The limit of a function at a point can be infinite! If a function decreases without bound from a given direction, then the one-sided limit is equal to

lim_{x \to a^{+}} f (x) = - \infty

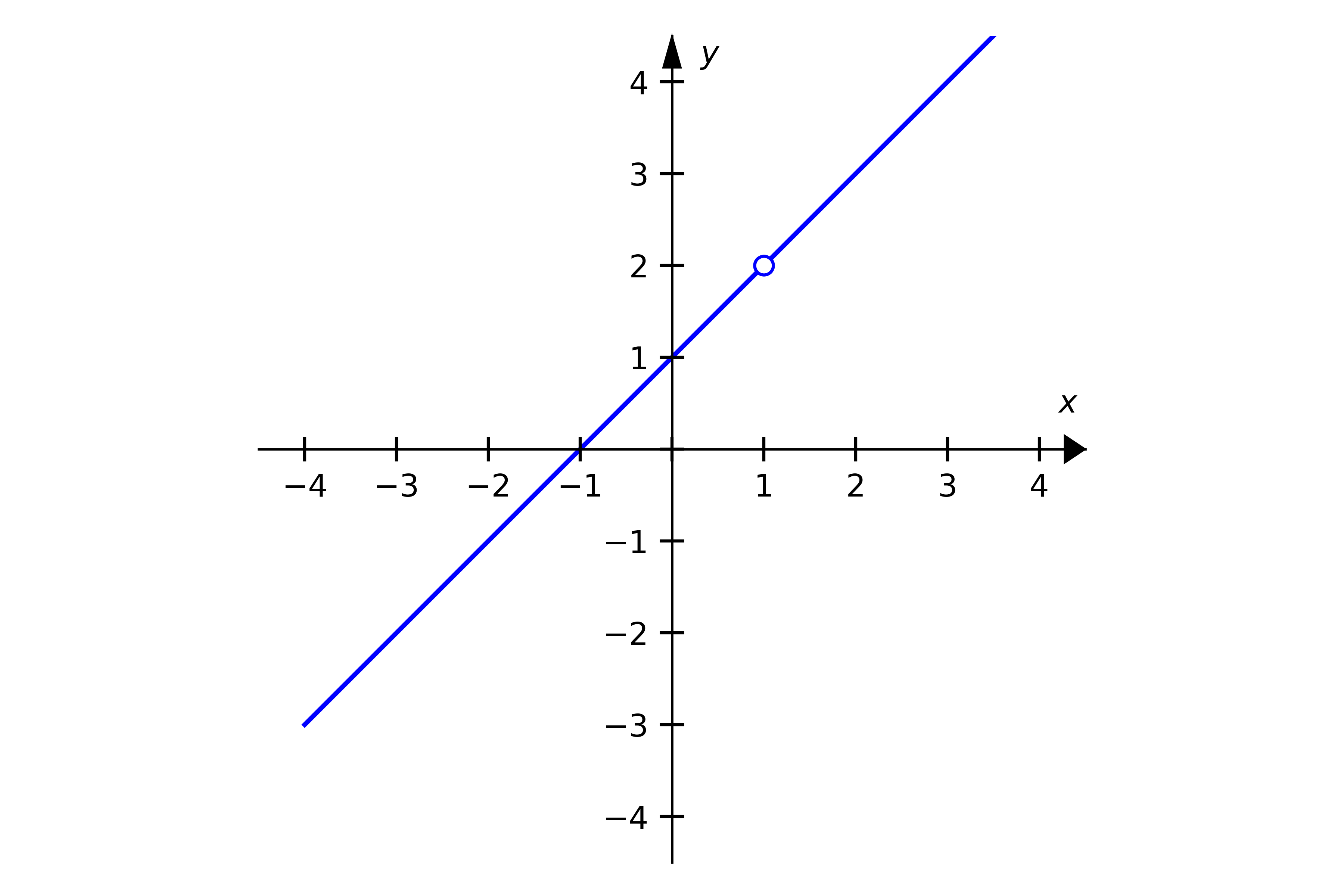
$graph$

(a) $f (x) = \frac{x}{x - 1}$

$graph$

(b) $f (x) = \frac{x^{2} - 1}{x - 1}$

$graph$

Figure 2: Functions undefined at x = 1.

lim_{x \to a^{-}} f (x) = - \infty

Instead, if the function increases without bound from a given direction, then its one-sided limit is equal to

lim_{x \to a^{+}} f (x) = + \infty

lim_{x \to a^{-}} f (x) = + \infty

Finally, as stated in the Theorem above, if the limits from both sides are the same (either both +∞ or both −∞), then we can write

lim_{x \to a} f (x) = - \infty

lim_{x \to a} f (x) = + \infty

Look at Figure 2a to see a great application of the principle of infinite limits.

Vertical Asymptotes: When the limit of a function tends to infinity at a point, the vertical line, x = a at that point is called a vertical asymptote of the function. Asymptotic behavior is generally undesirable in engineering applications as a range of values that crosses an asymptote will change very rapidly across the region close to the asymptote. Asymptotes are not restricted to a case where the left- and right-handed limits are equivalent. The example in Fig. 2a also represents a vertical asymptote, where the left-handed limit at x = 1 is negative infinity and the right-handed limit is positive infinity.

Practice

Determine the limit of the function at the point(s) given. Be as descriptive as possible!

Exercise 1. What can you say about the limit of this function at $x = 0$ ?

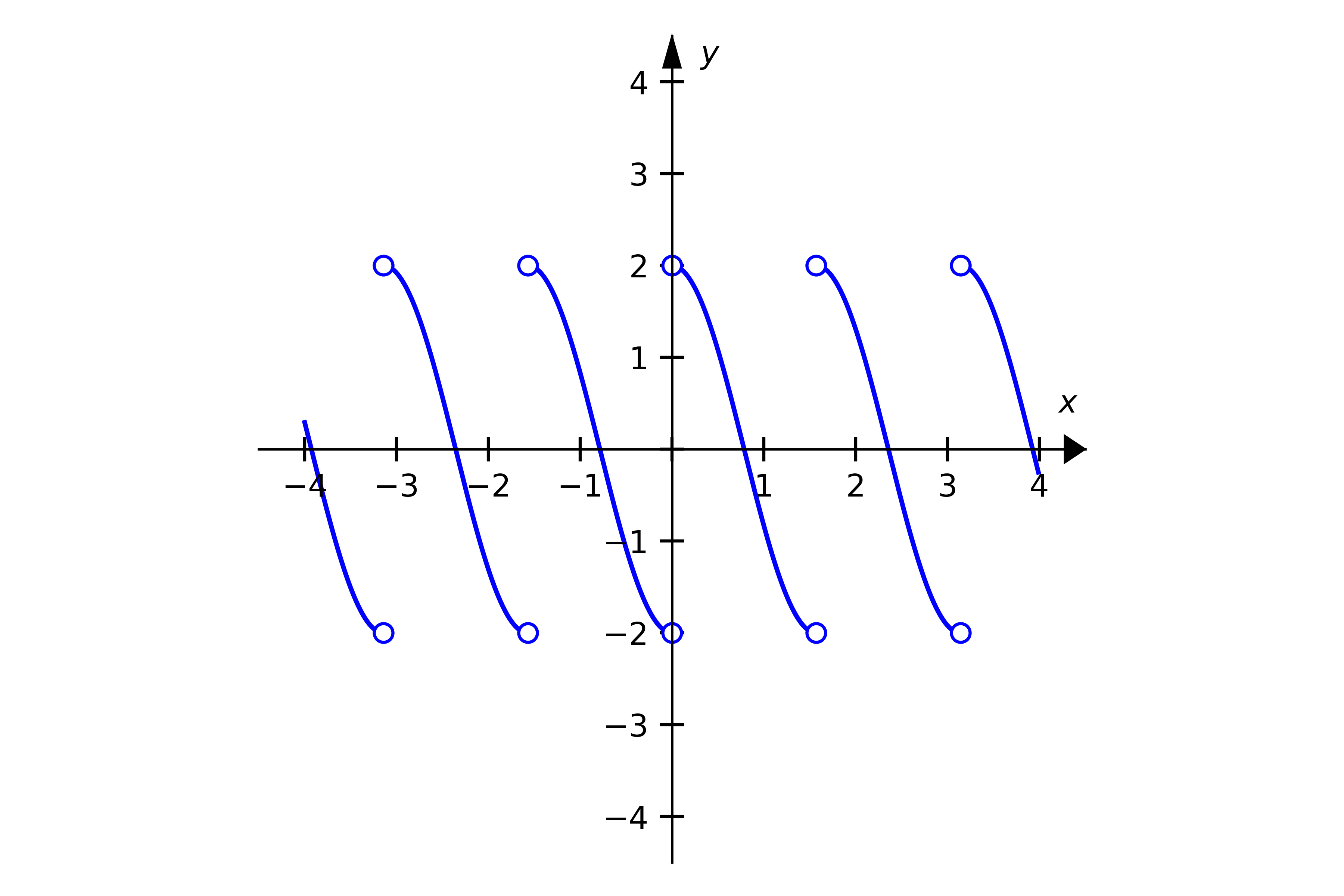
$graph for exercise 1$

Figure 3: $\frac{sin (4 x)}{|sin (2 x)|}$

Solution 1. At $x = 0$ , the limit of the function from the right is

lim_{x \to 0^{+}} = 2

and the limit of the function from the left is

lim_{x \to 0^{-}} = -2

Since the two one-sided limits are not the same, the limit at $x = 0$ does not exist, that is

$lim_{x \to 0} =$ D.N.E.

which is implied by Theorem 1. This function describes the derivative of the moment of inertia of an aircraft design with a rotating tail!

Limits

Engineering Context

The Essentials

A Deeper Dive

Practice

More Resources