Differentials
Engineering Context:
An understanding of differentials informs our understanding of the basics of calculus. Understanding differentials also helps us understand rates of change, an essential concept for engineers designing for dynamic systems. Although differentials seem to be a fairly theoretical concept on their own, they are an essential foundation of more advanced, highly applicable topics, such as calculus and differential equations. Differentials are also helpful when estimating values that are hard to calculate directly.
ECE: Differential equations, which relate a function to its own rate of change, are frequently used in electrical engineering, for example when finding the voltage across a capacitor based on the voltage applied to the circuit or determining input versus output voltage. Understanding differentials and rates of change is essential to understanding these differential equations.
BENG: For a biological engineer, one common application of rates of change is in reaction rates. Biological engineers are concerned with how fast certain enzymes can perform a given reaction, whether to produce a desired end product or to get rid of a certain reactant. An understanding of differentials would be important to understanding how fast or slow an enzymatic reaction occurs at a certain point in time.
CEE/MAE: As a civil or mechanical engineer working with physical measurements of spaces and structures, you want your measurements to be as error-free as possible. Differentials could help an engineer determine whether the possible error in their chosen measurement method is acceptable. For example, say a civil engineer is surveying a plot of land and they need to measure the area of the land within a certain allowable error. If they know the possible error of their distance measurements, they could use a differential form of the equation for area to determine whether or not their measurements will put them within their allowable error. The same sort of principle would be true for a mechanical engineer taking measurements for a design.
The Essentials
Differentials are, essentially, very small changes in input or output of a function. In calculus, they are typically considered to be infinitesimals (infinitely small in value). They are notated as da, with a being any letter (dy, dx, ds, etc). Conventionally, dx is the differential for a change in input and dy the one for a change in output.
dx can be thought of as an infinitely small ∆x and dy as an infinitely small ∆y. This association informs the use of differentials in the notation of a derivative, , as shown below:
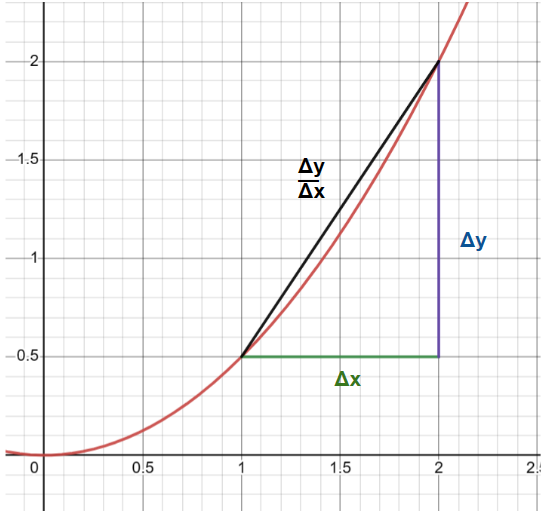
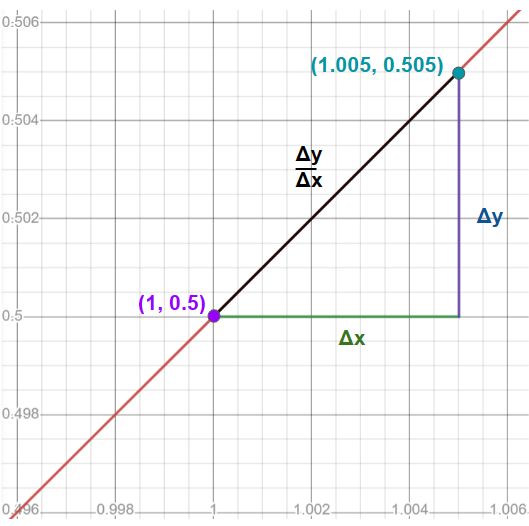
Figure 1: The graph , scaled normally on the left and zoomed in to the point (1, .05) on the right. As you zoom further in to this specific point and look at increasingly small values of ∆y and ∆x, those values will eventually become infinitely small differentials dy and dx, and the slope between them the derivative at the point (1, 0.5).
Differentials provide a method for estimating how much a function changes as a result of a small change in input. If , this equation can be rearranged to the differential form , which is similar to a linear equation ( is comparable to the slope m). Using the differential equation form, you can find a linear approximation of a function at a given point:
Solve: , , and
using given values,
which is the approximation for the function’s change in input when x changes by 0.1. The actual input change between x = 3 and x = 3.1 is:
which is very close to our approximated value of .9. Essentially what this equation is doing is taking the instantaneous slope at our initial point and assuming that that slope will be approximately constant across a small interval , from to .
Differentials can also be used to estimate error. If the actual value of some measured quantity is a but the measured quantity is , the error in any function of this quantity is , which can be approximated by .
A Deeper Dive
You can think of a derivative as a local analysis of the relationship between input and output around a certain point. In earlier math classes, we used to find the slope a function. Finding a derivative uses essentially the same process, but using infinitely small differential values for rise and run. Since slope of a function is given by or and since a derivative is thought of as an instantaneous slope, it would make sense that a derivative is the slope of an infinitely small interval, with an infinitely small change in y, dy, over an infinitely small change in x, dx.
Differentials are also used in the notation of an integral:
Here, the use of the differential dx emphasizes that an integral is an infinite sum of infinitely small quantities. We can see the significance of this notation when looking at the transition from Riemann sums to integrals. A Riemann sum approximates the area under a curve using the formula
on a closed interval . n refers to the number of subintervals the interval is divided into, i is the designation of each subinterval, a point anywhere on each subinterval, and ∆x is the width of each subinterval.
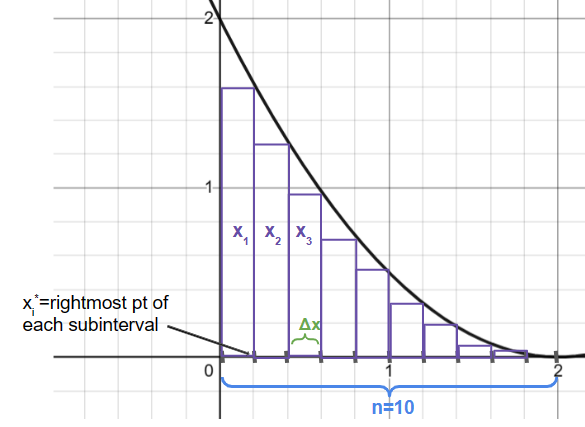
Figure 2: visual representation of a right-hand Riemann sum of on interval with
To get from a Riemann sum to an integral, take the limit of the sum as n goes to infinity:
As n, the number of subintervals, goes to infinity, ∆x will get smaller and smaller in value until it is the infinitely small differential dx. It is important that this differential value stay in the notation of an integral so we know which variable we are integrating with respect to – in this case, that we are taking the infinite sum of a function by summing infinitely small partitions of x. This notation comes in particularly handy when performing variable substitutions to compute integrals.
Practice
Exercise 1. If and , find dy at .
Exercise 2. If a cube is measured to have 5.0 inch sides with a possible measurement error of .1 inches, what is the estimated error of the volume of the cube?
Solution 1. Using the equation , . This is a good approximation for how much the function changes between x = 5 and x = 5.2.
Solution 2. Use the equation , where is the formula to calculate volume of a cube ( ), a is the side length of the cube (5), dx is error in initial measurement (.1), and dy = is estimated volume error. We will come out with dy = 7.803. This is approximately how much error a calculation for the volume of the cube will have if each side length has a full .1 inch error.

